How L-Systems Work ?

The Concept

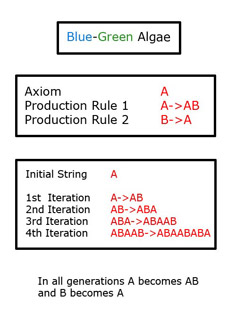
Aristid Lindenmayer, observed a plant during his research which is called anabaena catenula, a blue-green algae. The division process of the alga has been watched and noted that the cell has two states which will be represented as “A” and “B”. If the cell starts to grow from an initial state of A, it becomes “A” and “B” in the first division. In the second division “A” again, divides into “A” and “B”, and “B” becomes “A”. Figure_1 illustrates the division of an anabaena catenula, Blue-Green Algae cell by using the alphabet of L-Systems.

Rewriting

- Edge Rewriting

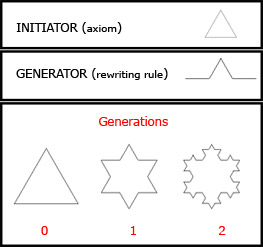
The main concept of the system is rewriting. Basically, this is a technique of replacing the parts of an initial object which will end up with a complex visual, by using a set of rules. And this is called “Edge Rewriting”. For the illustration purposes, a classical graphical object, a snowflake curve, will be given, that is proposed in 1905 by von Koch. Figure 2

- Node Rewriting

Apart from "Edge Rewriting" , there is another technique, called “Node Rewriting” which appends new parts instead of replacing the initial object.

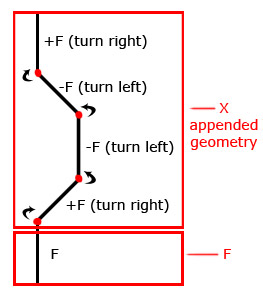
A simple L-System example for "Node Rewriting" with the real L-System Rules; Figure 3

L-System: Simple Example for Node Rewriting

Axiom     : FX
Rule        : X= +F-F-F+FX
Angle      : 45

As it can be seen from the example [Figure 3], L-systems starts with an initiator string which is called axiom. Then the system grows depending on the reproduction or the rewriting rules. So the rules determine how a given input string is transformed into an output string. Figure 4.

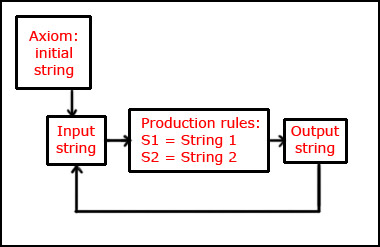
Figure 4 - L-Machine

As a characteristic of L-systems, there are divisions. Each divisions in the system is called “generations”.Since the L-Systems are string rewriting machines and the production rules applied simultaneously to all symbols of the input string, the system reflects a total biological property.

Graphical Interpretation of the L-Systems

Turtle Graphics:

The graphical interpretation of the L-Systems is based on Seymour Papert's concept of turtle graphics and especially suited for curves in the plane. To explain the logic of the turtle graphics, I want to quote a paragraph from the book of Peitgen, Jurgens and Saupe “ Fractals For The Classroom - Part Two: Complex Systems and Mandelbrot Set”;

" Let us imagine a turtle sitting on a sheet of paper facing in a certain direction. The tail of the turtle is a bit dirty. Thus, it leaves a trace on the paper as soon as the turtle starts to move. The turtle is thoroughly trained, it understands several commands, which we submit by remote control. The commands are given in the form of symbols (from the list of symbols used in the L-System). These symbols will be just ordinary letters from the alphabet and some special symbols such as + or -." (Page:34)

Figure 5 illustrates the graphical interpretation of a simple l-system with turtle graphics.

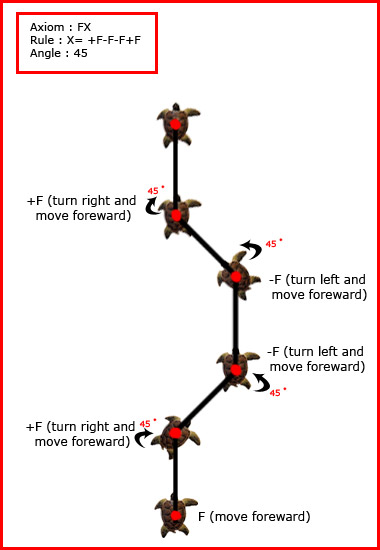
Figure 5 - Graphical Interpretation of a simple L-System